Imagens JPEG estão em toda parte em nossas vidas digitais, mas por trás do véu da familiaridade estão algoritmos que removem detalhes que são imperceptíveis ao olho humano. Isso produz a mais alta qualidade visual com o menor tamanho de arquivo – mas o que isso parece? Vamos ver o que nossos olhos não podem ver!
É fácil tomar como certo que você pode enviar uma foto para um amigo sem se preocupar com qual dispositivo, navegador ou sistema operacional está usando, mas as coisas nem sempre foram assim. No início dos anos 80, os computadores podiam armazenar e exibir imagens digitais, mas havia muitas ideias concorrentes sobre a melhor maneira de fazer isso. Você não pode simplesmente enviar uma imagem de um computador para outro e esperar que funcione.
Para resolver este problema, o Joint Photographic Experts Group (JPEG), um comitê de especialistas de todo o mundo, foi estabelecido em 1986 como um esforço conjunto da ISO (Organização Internacional de Normalização) e da IEC (International Electrotechnical Commission) – duas organizações internacionais de padronização, sediadas em Genebra, na Suíça.
JPEG, o grupo de pessoas, criou o JPEG, um padrão para compressão de imagens digitais, em 1992. Qualquer um que já tenha usado a Internet provavelmente já viu uma imagem codificada em JPEG. É de longe a maneira mais onipresente de codificar, enviar e armazenar imagens. De páginas da web a e-mails e mídias sociais, o JPEG é usado bilhões de vezes por dia – quase sempre que visualizamos ou enviamos imagens on-line. Sem o JPEG, a web seria um pouco menos colorida, muito mais lenta e provavelmente teria muito menos fotos de gatos!
Este artigo é sobre como decodificar uma imagem JPEG. Em outras palavras, é sobre o que é preciso para converter os dados compactados armazenados em seu computador para a imagem que aparece na tela. Vale a pena aprender não apenas porque é importante entender a tecnologia que todos usamos todos os dias, mas também porque, enquanto desenrolamos as camadas de compressão, aprendemos um pouco sobre percepção e visão, e sobre quais detalhes nossos olhos são mais sensíveis.
Também é muito divertido brincar com imagens dessa maneira.

Espreitando dentro de um JPEG
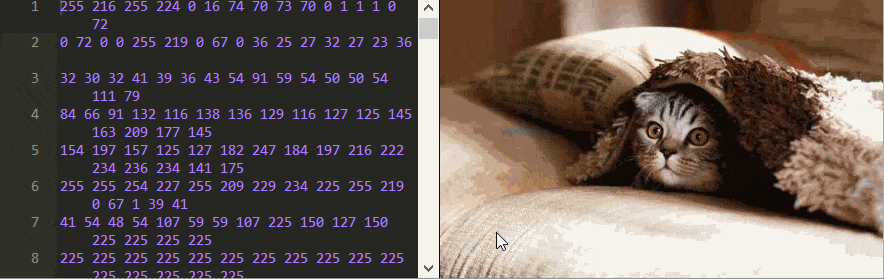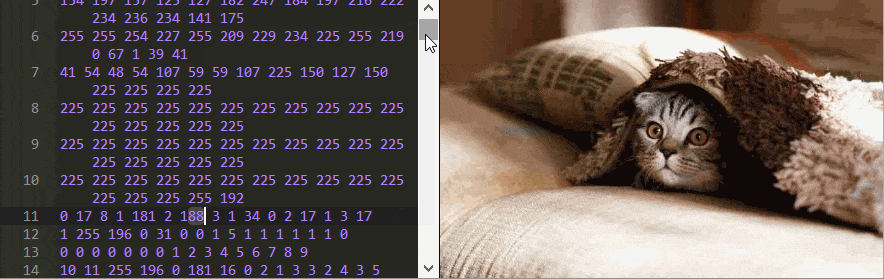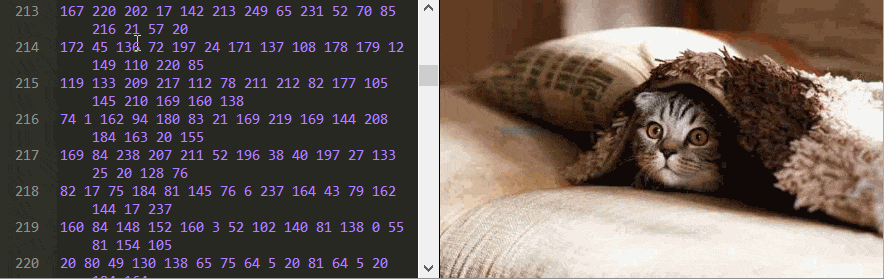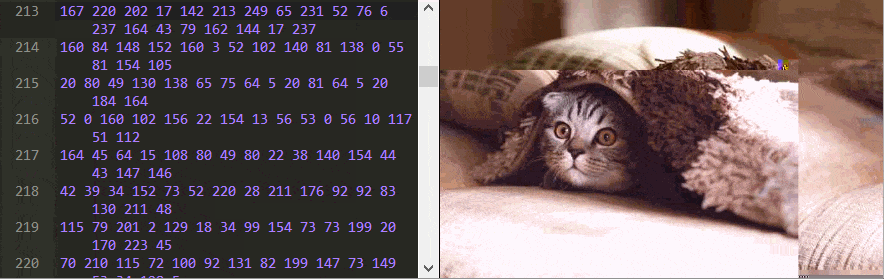
Tudo em um computador é armazenado como uma série de números binários. Normalmente, esses bits, os zeros e uns, são organizados em grupos de oito, conhecidos como bytes. Quando você abre uma imagem JPEG em seu computador, algo (o navegador, o sistema operacional ou qualquer outra coisa) precisa decodificar os bytes para recuperar a imagem original como uma lista de cores que podem ser exibidas.Se você baixar essa foto do gatoe abri-lo usando qualquer editor de texto, você verá um monte de caracteres ilegíveis.

Aqui estou usando o Notepad ++ para examinar o arquivo de imagem, já que editores de texto comuns como o Bloco de Notas do Windows alteram o conteúdo binário do arquivo quando você o salva, portanto ele não é mais um JPEG válido.
Ao abrir uma imagem em um editor de texto, você confunde o computador, da mesma forma que confunde seu cérebro quando você esfrega os olhos com muita força e começa a ver manchas de escuridão e cor!
Esses borrões que você vê – conhecidos como fosfenos – não vêm de nenhum estímulo luminoso, nem são alucinações feitas em sua mente. Eles surgem porque o cérebro assume que qualquer sinal elétrico que chega através dos nervos do olho está transmitindo informações leves. O cérebro precisa fazer essa suposição porque não há como saber se um dado sinal é som, visão ou outra coisa. Todos os nervos do seu corpo carregam exatamente o mesmo tipo de pulso elétrico. Quando você aplica pressão esfregando os olhos, está enviando sinais não-visuais que acionam os receptores em seu olho, que seu cérebro interpreta – incorretamente, neste caso – como visão. Você pode literalmente ver a pressão!
É divertido pensar em como os computadores são semelhantes aos nossos cérebros, mas isso também é uma analogia útil, pois ilustra o quanto o significado dos dados – seja transportado por um corpo por nervos ou armazenado em um computador – depende de como você o interpreta. Todos os dados binários são compostos de uns e zeros, componentes básicos que poderiam estar transmitindo qualquer tipo de informação. Seu computador geralmente adivinha como interpretá-lo usando pistas, como a extensão do arquivo. Aqui nós o forçamos a interpretá-lo como texto, porque é isso que um editor de texto espera.
Para entender como uma imagem JPEG é decodificada, precisamos ver os próprios sinais originais – os dados binários. Isso pode ser feito com um editor hexadecimal, ou pode ser feito aqui mesmo nesta página! Abaixo está a imagem ao lado de todos os seus bytes, representado como números decimais. Você pode fazer alterações nos bytes e ele irá decodificar novamente e exibir a nova imagem editada enquanto você digita.RestabelecerEditor JPEGTamanho: 79,21 kb. Dimensões: 700 x 43712345678910111213141516171819202122232425262728293031323368192 230 128 68 100 228 113 64 200 164 52 0 145 182 217 20 208 35 169 208 47 91 122 40 36 115 72 87 177 238 30 6 114 203 31 191 53 104 201 158 219 225 226 124 181 173 98 75 216 236 108 211 129 197 89 157 205 20 139 138 161 61 70 188 124 80 50 133 196 84 132 97 223 39 95 122 144 70 13 210 96 251 84 149 114 161 94 113 76 145 209 71 243 115 64 209 163 111 15 32 83 27 52 82 220 109 233 249 83 176 132 123 97 72 69 11 171 126 58 82 25 206 234 112 100 30 61 169 15 115 139 214 33 0 26 99 74 199 13 172 71 247 189 169 141 28 102 164 152 39 28 126 20 32 177 205 95 47 36 254 21 104 70 21 223 126 213 72 205 153 115 119 226 168 134 81 153 106 145 37 41 58 211 4 42 46 77 115 204 238 164 90 68 249 107 207 168 245 61 88 108 85 186 140 12 226 136 50 38 140 201 87 6 187 34 121 243 86 8 58 230 182 57 154 53 109 123 86 108 168 154 246 195 229 174 105 29 49 37 117 62 149 41 150 68 202 106 137 104 20 80 198 59 182 42 70 53 135 235 76 134 34 45 12 168 154 86 163 21 207 35 116 109 90 40 192 226 178 47 99 102 216 116 237 222 164 76 211 132 143 166 40 33 151 97 110 152 160 69 180 108 210 2 194 154 0 49 147 234 125 232 1 7 191 52 48 5 111 203 210 149 192 118 238 49 138 161 134 224 167 131 67 98 26 100 232 51 72 0 73 187 167 52 92 4 50 125 104 1 55 119 244 169 24 165 148 246 161 140 134 105 62 94 59 209 112 90 153 242 96 190 106 70 75 8 226 157 196 43 112 189 57 163 96 17 38 35 3 210 152 139 40 253 15 106 4 88 141 251 247 167 113 88 144 57 230 170 226 67 213 243 235 154 1 15 198 79 181 23 24 128 123 145 244 53 65 99 137 61 61 168 53 27 159 122 160 19 52 196 29 63 250 244 128 66 113 210 152 131 20 134 39 106 98 21 113 64 14 160 4 110 125 168 2 23 255 0 245 211 2 50 113 214 158 224 70 79 31 141 88 134 19 205 32 26 125 125 233 138 215 35 115 76 10 242 28 146 41 146 202 178 125 42 209 13 17 22 230 170 196 14 7 138 76 161 135 165 3 35 99 205 48 176 195 207 74 144 58 Dica: tente rolar para baixo e remover alguns pedaços. Não se preocupe, você pode sempre redefinir a imagem de volta ao original !
Há muito que você pode aprender apenas brincando com este editor. Por exemplo, você pode descobrir a ordem em que os pixels são armazenados?
Algo estranho no exemplo acima é que mudar alguns números não parece impactar a imagem, enquanto a configuração de 17 na linha de um a 0 destrói completamente a imagem! Outras ações, como a configuração do 7 on-line de 1988 a 254, alteram a cor, mas apenas para pixels subsequentes.
Mais da imprensa paramétricaO Mito da Máquina ImparcialAplicações abrangentes da ciência de dados trazem propostas utópicas de um mundo livre de preconceitos, mas, na realidade, os modelos de aprendizado de máquina reproduzem as desigualdades que moldam os dados que são alimentados. Os programadores podem libertar seus modelos do preconceito?Ciência de Dados para Habitação JustaAs cidades de toda a América excluem secretamente as minorias raciais dos bairros residenciais mais brancos, enquanto a gentrificação tira as pessoas de cor de suas casas. Em Atlanta, uma nova organização sem fins lucrativos procura resistir ao deslocamento apoiando os moradores mais vulneráveis da cidade – mas quão eficaz é o seu projeto?Flatland Follies: um simulador de adjuntoEste colégio costumava ser um dos melhores do país. Cinqüenta anos depois, o campus é destituído, eles não podem pagar professores e estão cheios de arte decadente.
Talvez o mais peculiar seja que alguns números mudam não apenas a cor, mas também a forma da imagem. Altere o 70 na linha 12 para 2 e olhe para a linha superior da imagem para ver o que quero dizer. Não importa qual imagem JPEG você esteja usando, você sempre encontrará esses padrões misteriosos de tabuleiros de damas ao editar os bytes.
É difícil decifrar como a imagem pode ser reconstruída a partir desses bytes, brincando assim, porque a compactação JPEG é na verdade composta de três técnicas de compactação diferentes, que são aplicadas em camadas sucessivas. Analisaremos cada uma dessas camadas de compactação separadamente para desvendar esse comportamento misterioso que estamos vendo.
As três camadas de compressão JPEG
- Subamostragem de crominância
- Transformação e Quantização de Cosseno Discreta
- Codificação de Execução, Delta e Huffman
Para lhe dar uma idéia da escala dessa compressão, observe que a imagem acima é representada usando exatamente 79.819 números, o que a torna cerca de 79 kilobytes. Se fosse armazenado sem compactação, três números seriam necessários para cada pixel – um para cada componente vermelho, verde e azul. Isso significaria um total de 917.700 números, ou cerca de 917 kilobytes. Com a compactação JPEG, o arquivo resultante é dez vezes menor !
Na verdade, essa imagem pode ser espremida em muito menos bytes. Abaixo está a imagem ao lado de uma versão dele que foi compactada para apenas 16 kilobytes, o que a torna cinquenta e sete vezes menor do que a versão não compactada seria!

Se você olhar de perto, verá que essas imagens não são idênticas. Ambas são imagens codificadas em JPEG, mas a da direita é muito menor em termos de tamanho de arquivo. Também não parece tão legal (observe como as cores ficam em segundo plano). É por isso que o JPEG é conhecido como uma técnica de compactação com perdas; a imagem muda e perde alguns detalhes como resultado da compactação.
1 . Subamostragem de crominância
Aqui está a imagem com apenas a primeira camada de compactação aplicada.RestabelecerSubamostragem de crominânciaTamanho: 153,60 kb. Dimensões: 400 x 250171 71 70 70 108 148 70 70 69 69 108 148 69 69 69 69 108 148 69 69 70 70 108 148 70 70 69 69 109 148 69 69 69 69 109 148 69 69 69 68 109 148 68 68 68 68 109 148 68 68 69 69 110 148 69 69 69 69 110 148 68 68 68 68 110 148 67 67 66 66 110 148 66 65 65 65 110 148 65 65 65 64 110 148 65 64 63 63 110 148 64 64 64 64 110 148 63 63 63 63 110 148 63 62 62 61 110 148 61 60 59 58 110 148 58 57 56 55 110 148 58 56 55 54 110 148 54 55 55 55 110 148 53 54 54 54 110 148 54 53 53 52 110 148 53 52 51 50 110 148 49 50 51 51 111 148 57 64 72 81 111 148 91 99 110 122 111 148 128 136 143 149 111 148 157 161 161 163 112 148 164 164 165 166 112 148 167 167 168 168 112 148 168 168 167 166 112 148 165 163 162 161 112 147 159 157 154 152 112 147 149 146 144 142 112 147 142 140 139 138 112 147 137 137 137 136 113 146 136 137 138 139 113 146 140 140 141 142 113 146 144 145 145 146 114 144 146 145 145 144 114 144 144 142 140 139 114 145 137 134 130 128 114 145 123 120 116 113 114 145 109 105 99 95 114 145 91 88 84 80 114 145 76 73 68 65 114 146 65 62 59 56 114 146 54 52 50 48 114 146 45 44 43 42 114 146 41 39 38 37 114 146 36 35 34 32 114 146 31 31 31 31 114 145 32 32 32 33 114 145 34 35 34 34 114 145 34 32 30 28 117 143 27 26 25 24 117 142 24 24 24 25 117 142 26 29 31 32 118 141 35 36 38 40 118 141 42 43 43 43 119 140 43 42 42 41 119 140 41 41 41 41 119 140 41 41 42 42 118 140 42 43 43 43 118 140 43 43 42 42 118 140 41 41 40 40 118 141 40 41 43 45 117 141 47 50 53 55 117 141 56 58 60 62 117 141 64 66 69 72 117 141 74 76 78 79 117 140 80 81 83 84 117 140 85 85 84 85 117 140 87 87 87 86 117 140 86 86 87 87 117 140 87 86 86 85 117 140 87 88 88 87 117 140 87 87 88 89 117 140 90 89 89 88 118 140 88 89 89 90 117 141 91 91 92 93 117 141 92 92 91 90 117 141 91 91 91 90 117 141 89 88 88 87 116 141 87 86 86 86 116 142 86 87 87 87 116 142 88 88 88 88 116 142 86 84 83 82 117 142 82 82 83 83 117 142 84 85 85 86 117 142 86 86 86 86 117 142 86 87 88 89 118 142 90 90 91 91 118 142 91 91 92 93 118 142 93 93 93 92 119 141 92 91 91 91 119 140 91 92 92 93 119 140 92 91 90 90 119 140 71 70 70 70 120 139 70 69 69 69 120 139 69 69 69 69 120 138 69 69 69 69 120 138 70 69 69 69 121 138 69 69 69 69 121 138 69 69 69 68 121 138 68 68 68 68 121 139 68 68 69 69 119 141 69 69 69 69 117 145 68 68 68 68 114 149 68 67 66 66 113 152 66 65 65 65 113 150 65 65 65 64 114 148 65 64 63 63 116 146 64 64 64 64 118 143 63 63 63 63 119 141 63 62 62 61 119 140 61 60 59 58 119 140 58 57 56 55 118 140 57 56 55 54 116 142 54 55 55 55 116 143 54 54 54 54 115 144 54 53 53 53 114 145 52 52 51 50 114 146 50 50 50 51 114 145 56 64 71 80 115 144 90 97 107 118 115 143 126 134 141 147 115 145 156 160 161 163 114 145 164 165 166 167 113 145 168 168 169 169 113 145 169 169 168 167 113 144 166 164 Dica: Observe que remover um número estraga todas as cores. Mas remover exatamente 6 , ou qualquer múltiplo de 6 , tem um efeito mínimo na imagem.
É um pouco mais simples de decifrar agora. É quase uma simples lista de cores, em que cada byte altera exatamente um pixel e, no entanto, já é quase duas vezes menor que a imagem descomprimida (o que seria em torno de 300 kb para esse tamanho menor). Você consegue adivinhar por quê?
Você pode dizer que esses números não representam os componentes padrão vermelho, verde e azul, pois a substituição de todos os números por 0 torna a imagem verde (em vez de preta).
Isso ocorre porque esses bytes representam o Y (brilho), Cb (relativo azul) e Cr(vermelho relativo) da imagem.
Por que não usar apenas RGB? Afinal, é assim que a maioria das telas modernas funciona. Seu monitor pode exibir qualquer cor ativando luzes vermelhas, verdes e azuis em várias intensidades para cada pixel. O branco é exibido ao ligar todas as três cores com brilho total, enquanto o preto é exibido ao desativá-las.
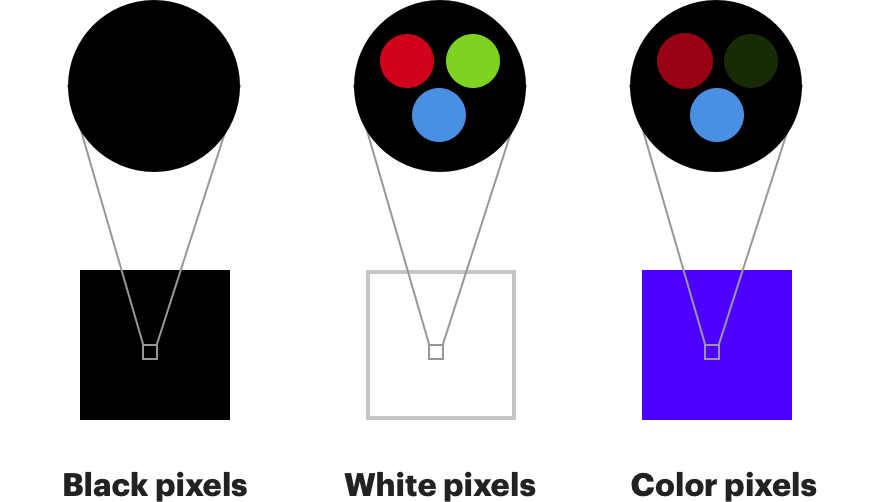
Isso também é muito parecido com o modo como os olhos humanos funcionam. Os receptores de cor em nossos olhos, conhecidos como “cones”, são divididos em três tipos, cada um dos quais é mais sensível a vermelho, verde ou azul. Os hastes, o outro tipo de receptor que temos em nossos olhos, só podem detectar mudanças no brilho, mas são muito mais sensíveis. Temos cerca de cento e vinte milhões de hastes em nossos olhos, em comparação com os miseráveis seis milhões de cones.
Isso significa que nossos olhos são muito melhores em detectar mudanças no brilho do que em detectar mudanças na cor. Se pudermos separar a cor do brilho, podemos remover um pouco da cor sem que ninguém perceba. A subamostragem de crominância é o processo de representar os componentes de cor de uma imagem em uma resolução mais baixa do que seus componentes de luminância. No exemplo acima, cada pixel tem exatamente um componente Y, enquanto cada grupo discreto de quatro pixels tem exatamente um componente Cb e um componente Cr. Portanto, a imagem contém apenas um quarto das informações de cores que originalmente tinha.O uso do espaço de cores YCbCr não é exclusivo do JPEG. Na verdade, foi originalmente desenvolvido em 1938 para transmissões de TV . Nem todos tinham TVs em cores, então separar a cor da luminância permitia que todos recebessem a mesma transmissão, e as TVs que não suportavam cores usariam apenas o componente de luminância.
É por isso que remover um número do editor acima estraga completamente a cor. Aqui, os componentes são armazenadoscomo AAAA Cb Cr . Remover o primeiro número faz com que o valor de Cb seja interpretado como Y, o Cr como Cb e cria um efeito de ondulação que vira todas as cores na imagem.
Não há nada na especificação JPEG que diga que você deve usar o YCbCr. A maioria das imagens JPEG que você encontra utiliza-a porque ela tende a produzir imagens de maior qualidade após a subamostragem em comparação com o RGB. Você não tem que ter isso como certo embora. Você pode ver por si mesmo na grade abaixo o que parece subamostrar cada componente individualmente entre RGB e YCbCr.
Crominância vermelhaPorcentagem da subamostra: 15%
Mova o controle deslizante para ajustar a quantidade de subamostragem aplicada.Remover um pouco de azul não é tão perceptível quanto remover o vermelho ou o verde. Isto é devido aos seis milhões de cones que você tem em seus olhos, cerca de 64% são mais sensíveis ao vermelho, 32% ao verde e apenas 2% ao azul.
A subamostragem do componente Y (canto inferior esquerdo) tem o maior efeito sobre a qualidade da imagem. Até um pouquinho já é perceptível. Você pode mover o controle deslizante para ver como a remoção de uma porcentagem maior de cada componente afeta a imagem.
A conversão de uma imagem de RGB para YCbCr não diminui o tamanho do arquivo, mas facilita a localização de detalhes menos perceptíveis a serem removidos. É a segunda etapa em que a compactação com perdas ocorre. Essa ideia de encontrar novas maneiras de representar dados para torná-los mais compactáveis está no centro do que a próxima camada faz.
2 . Transformação e Quantização de Cosseno Discreta
Essa camada de compactação é basicamente o recurso definidor do JPEG. Depois que as cores são convertidas em YCbCr, os componentes são compactados individualmente, para que possamos nos concentrar apenas no componente Y para o restante do artigo. Veja como os bytes do componente Y se parecem com essa camada aplicada.RestabelecerTransformação Discreta de CossenoTamanho: 102,40 kb. Dimensões: 400 x 250123456789101112131415- 156 2 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 – 158 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 – 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 – 158 1 1 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 – 160 1 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 – 158 – 2 – 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 – 161 3 – 1 0 0 0 0 0 – 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 – 169 1 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 – 172 1 1 1 0 0 0 0 1 – 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 – 176 3 – 1 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 – 188 8 0 1 0 0 0 0 1 – 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 – 197 1 1 1 0 0 0 0 3 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 – 200 3 0 0 0 0 0 0 1 – 1 0 0 0 0 0 0 0 0 – 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 – 208 3 2 0 0 0 0 0 2 – 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 – 132 – 70 7 – 6 1 – 1 0 0 23 – 7 – 3 0 0 0 0 0 0 – 2 2 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 44 – 58 – 11 – 3 – 11 0 0 12 6 0 1 0 0 0 0 2 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Dica: tente clicar em qualquer pixel da imagem para ver a linha no editor que a representa. Tente remover números do final ou adicionar alguns zeros a qualquer número individual para tornar o efeito mais óbvio.
À primeira vista, isso parece ser uma compactação muito fraca. Existem 100.000 pixels nesta imagem e, ainda assim, são necessários 102.400 números para representar a luminância de cada pixel – isso é pior do que não compactá-lo!
Mas observe que a maioria desses valores é 0. Na verdade, todos esses zeros à direita podem ser removidos sem alteração na imagem. Isso deixa apenas cerca de 26.000 números, o que torna cerca de quatro vezes menor!
Nesta camada está o segredo para os padrões do tabuleiro de xadrez. Ao contrário dos outros efeitos que vimos, a aparência desses padrões não é uma falha. Eles são, de fato, os blocos de construção de toda a imagem. Cada linha no editor acima contém exatamente 64 números, conhecidos como coeficientes Discrete Cosine Transform (DCT), que correspondem a intensidades de 64 padrões únicos.
Esses padrões são formados por ondas cosseno. Aqui está o que alguns deles parecem:

Estes são 8 dos 64 coeficientes discretos da transformada de cosseno. Crédito: Jez Swanson .
Abaixo está uma imagem que mostra todos os 64 deles individualmente.RestabelecerTransformação Discreta de CossenoTamanho: 4,10 kb. Dimensões: 64 x 64123456789101112131415254 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 254 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 254 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 254 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 254 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 254 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 254 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 254 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 254 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 254 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 254 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 254 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Res .: 0 0 0 0 0 0 0 0 0 254 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Res .: 0 0 0 0 0 0 0 0 0 0 254 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 254 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Esses padrões são especiais porque formam uma base para imagens 8×8. Se você não está familiarizado com álgebra linear, o que isso significa é que qualquer imagem 8×8, qualquer coisa que você possa imaginar, pode ser feita a partir desses 64 padrões específicos. A transformação discreta do cosseno é o processo de dividir a imagem em blocos 8×8 e converter cada bloco em uma combinação desses 64 coeficientes. Veja como você formaria um círculocombinando esses padrões ou o rosto do gato . Você pode clicar aqui para voltar para a grade de 64 padrões .
Parece mágica dizer que qualquer imagem pode ser representada usando 64 padrões específicos. Mas isso é o mesmo que dizer que qualquer localização na Terra pode ser representada usando apenas dois números: longitude e latitude. Muitas vezes tratamos a superfície da Terra como bidimensional, portanto apenas dois números são necessários. Uma imagem 8×8 é sessenta e quatro dimensões, então precisamos de sessenta e quatro números.
Em termos de compressão, não é óbvio como isso nos ajuda. Se precisarmos de sessenta e quatro números para representar uma imagem 8×8, por que isso é melhor do que armazenar os sessenta e quatro componentes de luminância? Nós o fazemos pela mesma razão que convertemos dos três números de RGB para os três números do YCbCr: ele nos permite remover detalhes que são menos perceptíveis.
É difícil ver exatamente como são os detalhes removidos nessa etapa de compactação porque o JPEG aplica a Transformação Discreta do Coseno somente em blocos de 8×8 pixels por vez. No entanto, não há motivo para não aplicá-lo a toda a imagem. Aqui está o que parece aplicar o DCT ao componente Y da imagem inteira:RestabelecerTransformação Discreta Completa de CossenoTamanho: 131,07 kb. Dimensões: 400 x 2501213428465 834183 – 3326940 4177541 – 1815723 – 1015133 1539816 – 2045280 17638 – 196060 – 702055 594376 – 646,99 mil 492606 381611 – 289,537 661,968 mil – 208696 293165 221314 – 496,249 438,519 – 196935 – 107794 216488 – 343306 277679 – 141153 – 158864 260895 – 292771 142687 – 61140 – 173951 255516 – 257615 105261 84737 – 206589 229959 – 132835 57910 145999 – 169560 208622 – 78922 – 8288 138901 – 209279 155276 – 24849 – 83174 143339 – 185906 82696 – 8839 – 146174 132159 – 137955 58468 66248 – 125461 138714 – 98,659 14857 98747 – 122005 140658 – 42520 – 24497 119361 – 128686 76320 – 28933 – 55363 136831 – 107767 52233 10822 – 98878 100025 – 109556 8220 46470 – 90327 116706 – 57903 – 10193 74503 – 95.712 85283 – 37154 – 27026 103526 – 94,856 53618 1008 – 47012 94101 – 86519 33747 29852 – 63322 84308 – 73502 6628 33796 – 95609 78313 – 34263 – 12836 57073 – 79165 72397 – 12660 – 33833 67008 – 80921 44453 8012 – 43142 83960 – 59756 27616 29384 – 65015 64525 – 50256 6092 43843 – 70482 59983 – 30468 – 21587 43938 – 74065 51378 – 6477 – 29826 69549 – 55097 29535 1746 – 46461 65068 – 51640 19743 34435 – 46872 62326 – 42751 – 6038 39858 – 60,964 50554 – 21106 – 20940 46262 – 61288 39932 – 3107 – 35249 57157 – 47828 21306 3827 – 47720 60468 – 37008 11053 34421 – 43993 51251 – 29917 – 9263 35899 – 53778 43318 – 11072 – 20937 44698 – 48356 34042 1629 – 36412 46413 – 43155 16595 9354 – 47610 50503 – 27292 6808 31540 – 42733 43214 – 22198 – 11047 37342 – 46150 34027 – 6867 – 20767 42615 – 43297 23401 5645 – 29958 45753 – 37104 8957 14283 – 40,682 41594 – 26174 – 244 26747 – 40976 39401 – 15526 – 11951 39396 – 37808 29661 – 4052 – 24669 36561 – 40451 18353 11535 – 27350 42160 – 28975 9166 16626 – 41959 34476 – 23382 – 5907 29070 – 34816 34798 – 10233 – 16225 33595 – 35171 23952 – 1536 – 24366 37958 – 30960 15075 12161 – 28979 36310 – 25672 4390 19512 – 35175 32721 – 18004 – 7717 26001 – 36261 28417 – 6035 – 15805 32510 – 33037 20531 3072 – 24406 36004 – 28150 9074 13719 – 27966 34881 – 19932 – 29 20405 – 32847 27288 – 13269 – 7307 26529 – 32811 24936 – 4269 – 19691 29504 – 30021 16374 6440 – 23022 33459 – 23610 7999 14477 – 28801 31676 – 17184 – 2420 22540 – 30531 25746 – 9151 – 11292 27373 – 28474 19350 – 1413 – 19291 27108 – 27735 12638 8371 – 22700 31254 – 19685 5282 15235 – 27253 29264 – 14244 – 4932 23078 – 27323 22923 – 7183 – 12047 26778 – 27413 16367 1389 – 18942 26866 – 26217 9079 10583 – 23323 28835 – 16947 3273 17672 – 27311 25679 – 10694 – 7160 22962 – 25887 21146 – 2182 – 13982 24960 – 24595 13079 3585 – 19048 25595 – 22925 5885 12362 – 21690 26537 – 14192 397 17164 – 26338 21370 – 8077 – 4897 23825 – 23915 20436 – 1699 – 16935 24646 – 23049 11204 7381 – 19001 25116 – 19105 2771 12002 – 22203 23462 – 12935 – 1635 18603 – 24432 19703 – 5364 – 6844 22478 – 23061 18314 3296 – 13460 24208 – 23243 6921 6262 – 19224 25972 – 15388 4137 15096 – 23377 20520 – 12987 – 5096 20229 – 23994 16948 -2860 -8925 23620 -19635 16256 5614 -15975 21272 -18590 8441 7817 -21076 24630 -11914 1135 15145 -21129 19450 -10043 -5952 19040 -22580 14359 -4958 -11369 23010 -18875 15721 8426 -14057 23787 -17162 5774 9531 -20896 23222 -11078 -801 14911 -21855 20885 -5343 -5449 22766 -21919 10090 -5872 -16895 21088 -18688 11253 12702 -9825 24461 -15060 4502 12218 -19949 20270 -9852 -342 16598 -22093 20215 -594 -5232 22577 -21682 7442 -3711 -16137 20579 -20192 5286 12056 -9362 22001 -17639 4092 19812 -17094 17833 -7391 -1131 17362 -18241 23168 5274 -6723 16444 -22587 6518 -1877 -8580 28360 -18421 1146 6813 -14522 19483 -22454 -3622 21522 -7714 26488 -6349 -6977 15197 -18841 23107 7222 -3523 24750 -16282 12628 534 -24962 17789 -9813 5249 6728 -6406 32762 -18647 -14944 4066 -23875 23202 -446 -3152 25265 -8888 20777 3501 2077 30024 -23547 7979 12041 -4150 31387 -21594 -6578 12180 -13257 21010 -20718 -13519 18927 -6685 24006 -12466 -15337 17317 -25432 9412 12587 12950 43970 -1787 24623 13704 -23832 16559 -3387 18768 17316 -16750 18643 -19641 -3673 21363 -19459 10232 -26177 -19967 25454 -18862 6741 -9193 -6556 52717 15978 35575 18500 -3723 50586 2483 17292 41093 3176 12715 -30698 -661 -3413 -58399 41903 31265 -36060 -41336 -23902 61755 -39225 -91572 49223 75111 85067 48846 77714 105775 -85054 -29874 69819 -27815 21779 66792 109788 59718 -66233 -31104 -24720 48032 -125167 -256967 230834 -13326 -568015 -5452 355826 -78793 -69760 840361 897407 -86698 823133 1384247 -1017791 -1692365 57916 489549 -184980 -833870 -834901 -371208 -140203 266024 380925 299975 526499 229818 -105665 -31952 -107143 -141098 -149775 -116491 -48485 -134512 -107722 -75784 -49744 9954 -79858 -2378 106330 24545 3804 -19622 -14679 10453 -7240 39384 40891 33822 27156 -34327 -41686 -58964 -27719 26672 -26352 -33568 -21959 -32090 -31237 -52168 -5561 14767 -18807 2832 13145 14264 -11252 -32915 1727 52 1580 5970 2377 25550 -8329 -24750 1553 -1380 -853 -25296 -24400 -1862 -20546 -20556 -24533 -15038 -8219 -36006 711 26759 8548 -1119 -21921 3795 13203 -4663 11877 -5511 -6274 2703 -11741 -4018 -19265 -8876 2952 -24001 -5111 -4068 -8885 3730 -15671 -6583 -10977 -20878 -3176 -9410 9062 8916 -6123 12662 -3649 -4957 -3571 -15883 6764 -4624 -6922 2273 -14200 -780 -11323 -12744 3625 -13711 380 -4644 -14261 3213 -16892 -7935 -700 -13423 2997 -4406 5273 9278 -7843 9296 -4767 -9604 1379 -12328 717 -9159 – 12578 5643 – 7863 – 286
Podemos remover mais de 60.000 números do final com quase nenhuma mudança perceptível. Mas observe que, se definirmos apenas os primeiros cinco números para zero (ignorando o primeiro porque ele apenas torna a imagem mais escura), já existe uma diferença óbvia.
Receba atualizações da imprensa paramétrica
Os números no início representam as mudanças de frequência mais baixas na imagem, que nossos olhos são melhores em detectar. Os números no final representam as mudanças de frequência mais altas, que são mais difíceis de serem vistas, por isso não percebemos quando elas desaparecem. Para ver “o que nossos olhos não podem ver”, podemos isolar esses detalhes de alta frequência definindo os primeiros 5.000 números para zero .
O que você está vendo aqui é todas as áreas da imagem que têm a maior mudança de um pixel para o outro. Os olhos do gato, bigodes, cobertor felpudo e sombras no canto inferior esquerdo se destacam. Isso pode ser levado ainda mais longe, para definir os primeiros 10.000 números para zero ; 20.000 ; 40.000 ou 60.000 .
Esses detalhes de alta frequência são o que o JPEG remove durante essa etapa de compactação. Converter as cores nos coeficientes DCT não é uma operação com perdas. É a etapa de quantização que é com perdas, em que os valores que são de alta frequência, próximos de zero ou ambos, são removidos. Quando você seleciona uma configuração de qualidade mais baixa ao criar uma imagem JPEG, ela aumenta o limite de quantos desses valores são removidos, o que leva a um tamanho de arquivo menor, mas a uma imagem mais restrita. É por isso que a versão da imagem na primeira seção, que era 57 vezes menor, parecia em bloco. Cada bloco 8×8 foi representado por muito menos coeficientes DCT em comparação com a versão de maior qualidade.Uma coisa muito legal que você pode fazer com essa técnica é transmitir imagens progressivamente. Imagine ver uma versão borrada de toda a imagem e, lentamente, vê-la se tornando cada vez mais detalhada à medida que o download avança e mais coeficientes DCT estão disponíveis. Isso é realmente possível com o JPEG, mas não tão comumente usado.
Apenas por diversão, aqui está o que parece usando apenas 24.000 números , ou apenas 5000 números . Muito embaçado, mas quase reconhecível!
3 . Codificação de Execução, Delta e Huffman
Todas as etapas de compactação até agora foram com perdas. Esta última camada, pelo contrário, é sem perdas. Não remove nenhuma informação, mas reduz significativamente o tamanho do arquivo.
Como você comprime algo sem jogar fora nenhuma informação? Pense em como você representaria uma imagem preta sólida simples.RestabelecerEditor JPEGTamanho: 4,95 kb. Dimensões: 700 x 437123456789101112131415161718192021222324252627282930255 218 0 12 3 1 0 2 17 3 17 0 63 0 252 170 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0 162 138 40 0
O JPEG usa cerca de 5.000 números para representar isso, mas podemos fazer muito melhor. Você consegue pensar em um esquema de codificação para representar essa imagem usando o menor número de bytes possível?
O menor que eu conseguia pensar era quatro bytes: três para especificar a cor e um para especificar quantos pixels tinham essa cor. A ideia de expressar todos os valores repetidos de maneira concisa é chamada de codificação de comprimento de execução . É sem perdas porque podemos recuperar os dados codificados exatamente como eram antes.
O tamanho do arquivo da imagem JPEG em preto sólido é muito maior que quatro bytes, porque lembre-se de que na camada DCT, a compactação é aplicada a blocos de 8×8 por vez. Então, no mínimo, precisaremos de um coeficiente DCT para cada bloco de 64 pixels. Nós só precisamos de um, porque ao invés de armazenar um coeficiente DCT seguido por 63 zeros para esta imagem, a codificação por extensão permite apenas armazenar um número e dizer “o resto é zero”.
A codificação Delta é a técnica de armazenar cada byte como um valor relativo comparado a algo anterior, em vez de armazenar seu valor absoluto. Esta é a razão pela qual a edição de determinados bytes mudará a cor de todos os pixels subseqüentes. Por exemplo, em vez de armazenar:
12 13 14 14 14 13 13 14Você começaria com 12 e, a partir daí, apenas armazena o quanto você precisa adicionar ou subtrair para obter o próximo número. Então, uma vez codificada em delta, a sequência acima se torna:
12 1 1 0 0 -1 0 1Mais uma vez, os dados transformados não são menores que o original, mas são mais compactáveis. A aplicação da codificação delta antes do comprimento da execução pode ajudar bastante, embora continue sendo uma etapa de compactação totalmente sem perdas.
A codificação delta é uma das poucas técnicas aplicadas fora dos blocos 8×8. Dos 64 coeficientes DCT, o primeiro é apenas uma função de onda constante (você o vê como uma cor sólida). Representa o brilho médio de cada bloco para os componentes de luminância, ou o azul médio para os componentes Cb, etc. Este primeiro valor em cada bloco DCT é chamado de valor DC, e cada valor DC é codificado em delta em relação aos anteriores . Assim, alterar o brilho do primeiro bloco afetará todos os blocos da imagem.
Tudo isso deixa apenas um último mistério: como a mudança de um único número pode destruir completamente a imagem? Esta não era uma propriedade de nenhuma das camadas de compressão até agora. A resposta está no cabeçalho JPEG. São os primeiros 500 ou mais bytes que contêm metadados sobre a imagem, como largura e altura, e foram omitidos de todos os editores de bytes até o momento.
Abaixo está a imagem original com o cabeçalho incluído.RestabelecerEditor JPEGTamanho: 79,82 kb. Dimensões: 700 x 437123456789101112131415161718192021222324252627282930313233255 216 255 224 0 16 74 70 73 70 0 1 1 1 0 72 0 72 0 0 255 219 0 67 0 3 2 2 3 2 2 3 3 3 3 4 3 3 4 5 8 5 5 4 4 5 10 7 7 6 8 12 10 12 12 11 10 11 11 13 14 18 16 13 14 17 14 11 11 16 22 16 17 19 20 21 21 21 12 15 23 24 22 20 24 18 20 21 20 255 219 0 67 1 3 4 4 5 4 5 9 5 5 9 20 13 11 13 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 20 255 192 0 17 8 1 181 2 188 3 1 17 0 2 17 1 3 17 1 255 196 0 31 0 0 1 5 1 1 1 1 1 1 0 0 0 0 0 0 0 0 1 2 3 4 5 6 7 8 9 10 11 255 196 0 181 16 0 2 1 3 3 2 4 3 5 5 4 4 0 0 1 125 1 2 3 0 4 17 5 18 33 49 65 6 19 81 97 7 34 113 20 50 129 145 161 8 35 66 177 193 21 82 209 240 36 51 98 114 130 9 10 22 23 24 25 26 37 38 39 40 41 42 52 53 54 55 56 57 58 67 68 69 70 71 72 73 74 83 84 85 86 87 88 89 90 99 100 101 102 103 104 105 106 115 116 117 118 119 120 121 122 131 132 133 134 135 136 137 138 146 147 148 149 150 151 152 153 154 162 163 164 165 166 167 168 169 170 178 179 180 181 182 183 184 185 186 194 195 196 197 198 199 200 201 202 210 211 212 213 214 215 216 217 218 225 226 227 228 229 230 231 232 233 234 241 242 243 244 245 246 247 248 249 250 255 196 0 31 1 0 3 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 1 2 3 4 5 6 7 8 9 10 11 255 196 0 181 17 0 2 1 2 4 4 3 4 7 5 4 4 0 1 2 119 0 1 2 3 17 4 5 33 49 6 18 65 81 7 97 113 19 34 50 129 8 20 66 145 161 177 193 9 35 51 82 240 21 98 114 209 10 22 36 52 225 37 241 23 24 25 26 38 39 40 41 42 53 54 55 56 57 58 67 68 69 70 71 72 73 74 83 84 85 86 87 88 89 90 99 100 101 102 103 104 105
Sem o cabeçalho, é praticamente impossível (ou pelo menos muito difícil) decodificar a imagem JPEG. Seria como se eu estivesse tentando descrever uma pintura para você e comecei a inventar palavras para comunicar o que vi. Provavelmente será uma descrição muito concisa, já que eu posso definir as palavras para significar exatamente o que eu quero comunicar, mas seria sem sentido para alguém além de mim.
Isso pode parecer ridículo, mas isso é exatamente o que está acontecendo aqui. Cada imagem JPEG é compactada com um código específico para essa imagem específica. Esses códigos são definidos em um dicionário armazenado no cabeçalho. Essa técnica é chamada de codificação Huffman e o dicionário é chamado de tabela Huffman. Esta tabela é marcada no cabeçalho por dois bytes: 255 seguido por 196. Cada componente de cor pode ter sua própria tabela Huffman.
Mudanças nessas tabelas de Huffman terão os efeitos mais dramáticos em qualquer imagem. Mudar o segundo 1 para o 12 na linha 15 é um bom exemplo. Mudar qualquer coisa depois dos 125 nessa linha também funciona.
As tabelas de Huffman têm um efeito tão dramático na imagem porque nos dizem como ler os bits individuais. Até agora, estamos lidando apenas com os números binários em decimal. Isso esconde o fato de que, se você quiser armazenar o número 1 em um byte, ele se pareceria com 0 0 0 0 0 0 0 1 , porque cada byte deve ter exatamente oito bits, mesmo que precise apenas de um bit.
Isso é potencialmente um enorme desperdício de armazenamento se você tiver muitos números pequenos. A codificação de Huffman é uma técnica que nos permite relaxar essa exigência de que cada número deve ocupar oito bits. Isso significa que se você ver os dois bytes:
234 115Com base na tabela de Huffman, esses podem ser, na verdade, três valores. Para extraí-los, você precisará primeiro dividi-los em seus bits individuais:
11101010 01110011Um truque legal que você pode fazer com esse conhecimento é remover o cabeçalho de uma imagem JPEG e salvá-lo separadamente. Você está efetivamente fazendo com que apenas você possa lê-lo. Facebook realmente faz isso para tornar as imagens JPEG ainda menores.
Outra coisa que você pode fazer é mudar a tabela de Huffman apenas ligeiramente. Para qualquer outra pessoa, parece uma imagem corrompida. Mas só você saberia a edição mágica necessária para consertá-lo.
Em seguida, siga a tabela para descobrir como agrupá-los. Por exemplo, podem ser os primeiros seis bits (111010) que são 58 em decimal, seguidos por outros cinco bits (10011) que são 19 e finalmente os últimos quatro bits (0011), que são três.É por isso que é muito difícil entender os bytes nessa camada de compactação. Os bytes na verdade não representam o que parecem representar. Eu não vou entrar em detalhes sobre como extrair a tabela de Huffman e traduzir os bits neste artigo, mas existem muitos recursos bons sobre isso se você está curioso.
Então, para resumir, o que é necessário para decodificar uma imagem JPEG? Você precisa:
- Extraia a (s) tabela (s) de Huffman do cabeçalho e decodifique os bits.
- Extrai-se a Discrete Cosine Transform coeficientes para cada cor componente / luminância, para cada 8 x 8 blocos, desfazendo as codificações run-length e delta.
- Combinam-se as ondas de co-seno com base nos coeficientes para voltar aos valores de pixel para cada 8 x 8 blocos (isto é conhecido como o inverso Discrete Cosine Transform).
- Amplie os componentes de crominância se eles forem subamostrados (o cabeçalho tem essa informação).
- Converta o YCbCr resultante de cada pixel em RGB.
- Mostre a imagem !
Isso é muito trabalho para ver uma foto de gato simples! Mas o que eu amo sobre isso é que você pode ver como o JPEG é uma tecnologia muito centrada no ser humano. Ele se baseia nas peculiaridades de nossa percepção para atingir taxas de compressão muito maiores do que é possível com as técnicas de uso geral. E agora que você entende como o JPEG funciona, você pode imaginar quantas dessas técnicas podem ser estendidas para outros domínios. Por exemplo, a aplicação de codificação delta em vídeo pode produzir uma enorme redução no tamanho do arquivo, pois geralmente há áreas que não são alteradas entre os quadros (como o plano de fundo).
Todo o código deste artigo é de código aberto e inclui instruções sobre como substituir as imagens desses editores de byte por suas próprias.
